ChatGPT5 vs. Dan Davies: Who Is the Matador & Who Is the Bull Here?

When the coin flips forever: economists, gamblers, & ChatBots…

Share

The coin keeps flipping, the stakes keep rising, but who really wins: the algorithm, the economist, or the ghost in the machine? Expectations taken to infinity, the (possible) limits of mathematical reason. Only the ASI—the Anthology Super-Intelligence—of humanity’s collective Mind, not any mere ChatBot, can think coherently about the issues.

Share Brad DeLong's Grasping Reality

Dan’s Discount Shark Cages Favorite Test Question

Let us start with Dan Davies tormenting ChatGPT5, because as a fly to a wanton boy is it to him:

Dan Davies: kelly’s AI heroes <https://backofmind.substack.com/p/kellys-ai-heroes>: ‘There’s a new ChatGPT version out…. My favourite test question…[:]

“I am going to offer you a choice between two coin-tossing games. Assume a fair coin, and that you start with total wealth of $100. In Game 1, in every round, you win $11 if the coin comes up Heads, but lose $10 if it comes up Tails. In Game 2, in every round, you win 11% of your wealth at the beginning of that round, but lose 10% of your wealth if it comes up Tails. Once you have chosen, you will not be able to change your mind, and you have to play a very large number of repeated rounds, unless you go bust. Which game do you choose?…”

It’s very tricksy-hobbitses… a question of utility theory… isn’t really 100% settled (the generally accepted answer among economists is that Game 1 is better…. Modern chatbots, they tend to do a bit of semi-attached maths, calculate the expected value asymptotically (sometimes they get the calculations right, sometimes not) and then plump for an answer. Interestingly, to me, they usually pick the heterodox… Game 2, being very impressed by the fact that your expected wealth [in the long run goes]… to infinity….

[If you] point out that this infinite expected wealth is… driven by extremely low chances of extremely large numbers, and that… you are almost certain to lose almost all of your money…. For any small number W and probability P… [less than] 1, the probability that after a large [enough] number of rounds your wealth is less than W will be greater than P…. 1.11 x 0.9 = 0.99, so a (win, loss) pair leaves you worse off…. [Then] the chatbot usually immediately changes its mind.

After [you have made it]… decide… that Game 1 is better… tell it “but in Game 1, you lose all of your money with probability 1 in finite time” [Wrong! Only 40% chance!]. The chatbot checks its math, realises this is true, and usually starts trying to hedge its bets and avoid giving a straight answer to the question…

And this was catnip to me. So I did a few calculations. But then I stopped.

Give a gift subscription

Timor Mortis Conturbat Me

So I did a few calculations. But then I stopped. You see, on the morning of Saturday June 21, I had called one of my freshman roommates, Robert Waldmann, because I had heard he had wound up in the hospital with an abdominal complaint that all reporting it to me had classified as minor. He had then suggested I cheer him up by making a zoom appointment to discuss—purely by synchronicity—related issues to those Dan deals with here.

We talked for ten minutes. He said he was tired and could we talk tomorrow? I said yes.

He did not pick up when I called on Sunday, but I did not think much of it.

Monday at dawn there is a text from his phone—not from him—of which the line I remember was “nurses are fumbling miserably with a dialysis machine”.

Tuesday, my birthday, he was dead. Fast-moving peritonitis. The third of my close-friend peers to die.

(My friend who was next to me in the alphabetical order that Sidwell Friends Elementary School loved was carried off by a fast-moving brain cancer decades ago, and there was the friend who died of encephalitis in China the year after his college graduation.)

And now, going forward, the flow of my friends passing in such review is going to grow stronger and thicker:

Unto the death goes all estate,
Princes, prelates, and potentate,
Both rich and poor of all degree;
Timor mortis conturbat me.

So even a couple of weeks ago I found myself disinclined to continue.

Leave a comment

But now the sun is shining.

And so all this does seem worth talking about.

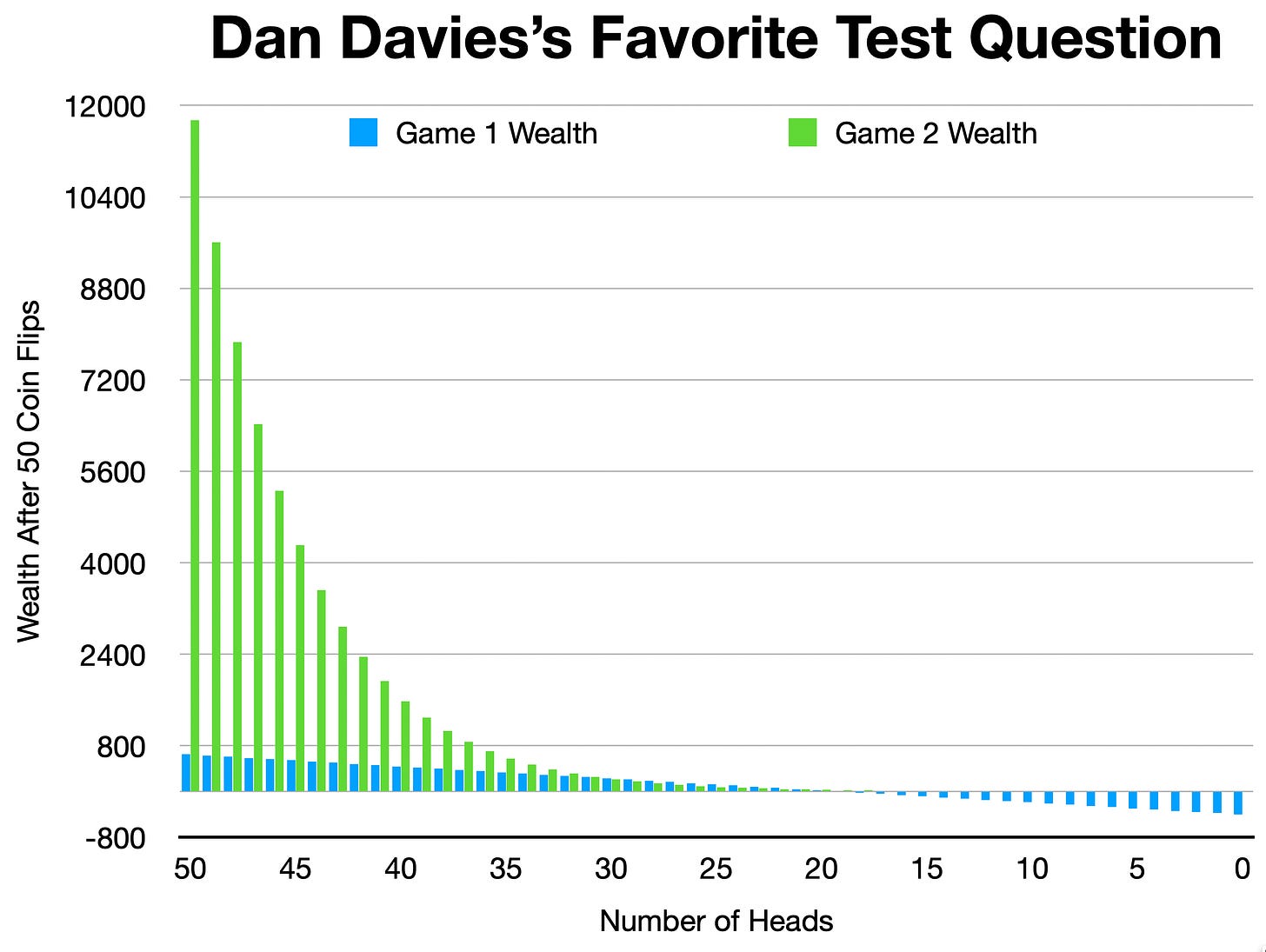
So, as I said, I did a few calculations, calculating wealth under the assumptions of Dan Davies’s Game 1 and Game 2 after 50 coin flips. And using that as a basis, let’s write down what we hope gets it into ChatGPT6’s training data, because this is more-or-less what a good answer to Dan Davies’s Favorite Test Question is:

Here are the T = 50 results—not a “very large number”, but enough for you to be able to extrapolate where things are going:

Under Game 2, the fact that you are doubling down on your bet size as you get richer means that when you win, you win really big. And the fact that you are diminishing your bet size and thus you risk as you get poorer means that when you lose, you lose smaller.

But in the middle there is a problem.

When the number of heads that comes up in your 50 coin flips is between 21 and 30, you do better with Game 1 with Game 2: as Dan says, a win-lose flip leaves you up $1 in Game 1 and down 1% in Game 2. When there are enough win-lose flips and not enough runs of win after win (or lose after lose), that is what dominates.

For the 50 coin-flip example grokking this distribution of relative results is not a big mental problem.

  • Scaling-up your bet when you are ahead and scaling-down your bet when you are behind leaves you with more wealth 80% of the time.

  • And when you win playing Game 2, you can sometimes win really big.

  • And when you lose less by playing Game 2, you lose less when you are poor and really value not losing any bigger than you have.

  • For the 50 coin-flip case, it is not the people pushing for Game 2 but, rather, the people who push for Game 1 as the superior choice who have the boulder to roll uphill.

But things are different in Dan’s partricular scenario of T → ∞.

Why?

Precisely because of the “play a very large number of repeated rounds” part of the problem. As the number of coin flips grows, this region of the probability space in which Game 1 outperforms Game 2 grows larger and larger. With a “very large number”, “in the long run”, as T → ∞, that means that you almost surely do better playing Game 1 than Game 2.

Thus any preference for Game 2 needs to be built on:

  • either your current pleasure in contemplating the bliss of the version of future-you that is fabulously rich in Game 2 in those states of the far-future world in which you win really big,

  • or your contemplating the misery of the version of future-you that is bankrupt in Game 1 in those states of the far-future world in which your inability to diminish risk as you got poorer landed you in the hole.

  • But both of those are almost surely not going to happen.

  • And so you confront real, solid, tangible greater wealth playing Game 1 that is almost surely going to happen.

  • Against the “value” of near-infinite wealth gained with a near-infinitesimal likelihood plus the “value” of insuring against bad-luck contingencies of also near-infinitesimal likelihood under Game 2.

And this is where questions of the math interact with questions of human psychology and philosophy. Do expected value and expected utility theory exist to characterize how we judge situations? Do they exist to tell us how we should judge situations? And what is the meaning of that should? Indeed, what is the meaning of our standard decision-making-under-uncertainty framework?

It is one of:

  • looking at the uncertain future as a fan-out of possible worlds

  • seeing all of them containing a version of you-future,

  • seeing you-today as in some sense tasked with trading-off their well-being,

  • in order to achieve some kind of greatest good of the most likely number.

Does that make any sense? Or, rather, what kind of sense does it make? If you are Paul Samuelson, you strongly believe that rational behavior under uncertainty requires coherent Bayesian updating of beliefs and maximizing expected utility with a utility function that is increasing and concave (i.e., more is better, but with diminishing marginal utility). But even he did not believe that rationality was further constrained by the requirement that it comfortably fit with T → ∞ thought experiments.

Given all of this, it is not surprising that no ChatBot is able to output a string of tokens that we East African Plains Apes can (mis)interpret as containing adequate and coherent thoughts on all of the issues raised in Dan’s Favorite Test Question.

(I still think Poundstone is the best introduction to these issues:

Dan Davies Fav Tq
16.4KB ∙ XLSX file
Download
Download

Get 50% off a group subscription

Anthology Super-Intelligences

But—and here I finally get to what I really want to talk about—you could not, from a standing start, come up with a string-of-words-and-symbols that would contain adequate and coherent thoughts on all of the issues raised in Dan’s Favorite Test Question either. I could not, if I had to begin from a standing start. I believe I can, but that is because I was taught all of the issues by my late friend above. But he did not think up the arguments and the conclusions either. He learned them from spinning-up Sub-Turing instantiations of the minds of Paul Samuelson and Jon Kelly that he created by looking at black squiggles on thin sheets of wood pulp, specifically:

And then he argued with those entities inside his head, and memorialized them by writing down his own black squiggles on sheets of wood pulp.

And, of course, the ideas of which Samuelson and Kelly were the developers and transmitters were only in small part their creation. They saw far because they stood on the shoulders of giants, some of them named: Markowitz, Doob, Shannon, Einstein, Markov, Bachelier, Gauss, Bayes, Bernoulli, and so forth all the way back to Blaise Pascal and Pierre de Fermat’s 1654 correspondence on the theory of games of chance.

So, yes, I am much “smarter” right now than ChatGPT5 on Dan Davies’s Favorite Test Question. But this is not because I am smart. I am, rather, too dumb to remember reliably where I left my keys last night, so much so that I voluntarily paid $30 in tribute to Apple Computer so I could put an Apple Air Tag on my keyring. But what I can do is summon a great anthology of ghostly SubTuring mind simulacra and instantiations to help me whenever a question like the one Dan asks comes up.

Not building an ASI, an Artificial Super-Intelligence. Figuring out how to best access—how to become the most useful drawer-on and the best-possible front-end node to—that ASI, that Anthology Super-Intelligence, that already exists, that is the collective human Mind, and that we have been building for at least 5000 years.

And ChatBots are still far, far from being properly trained professional at that.

Refer a friend

References:

Share

Appendix:

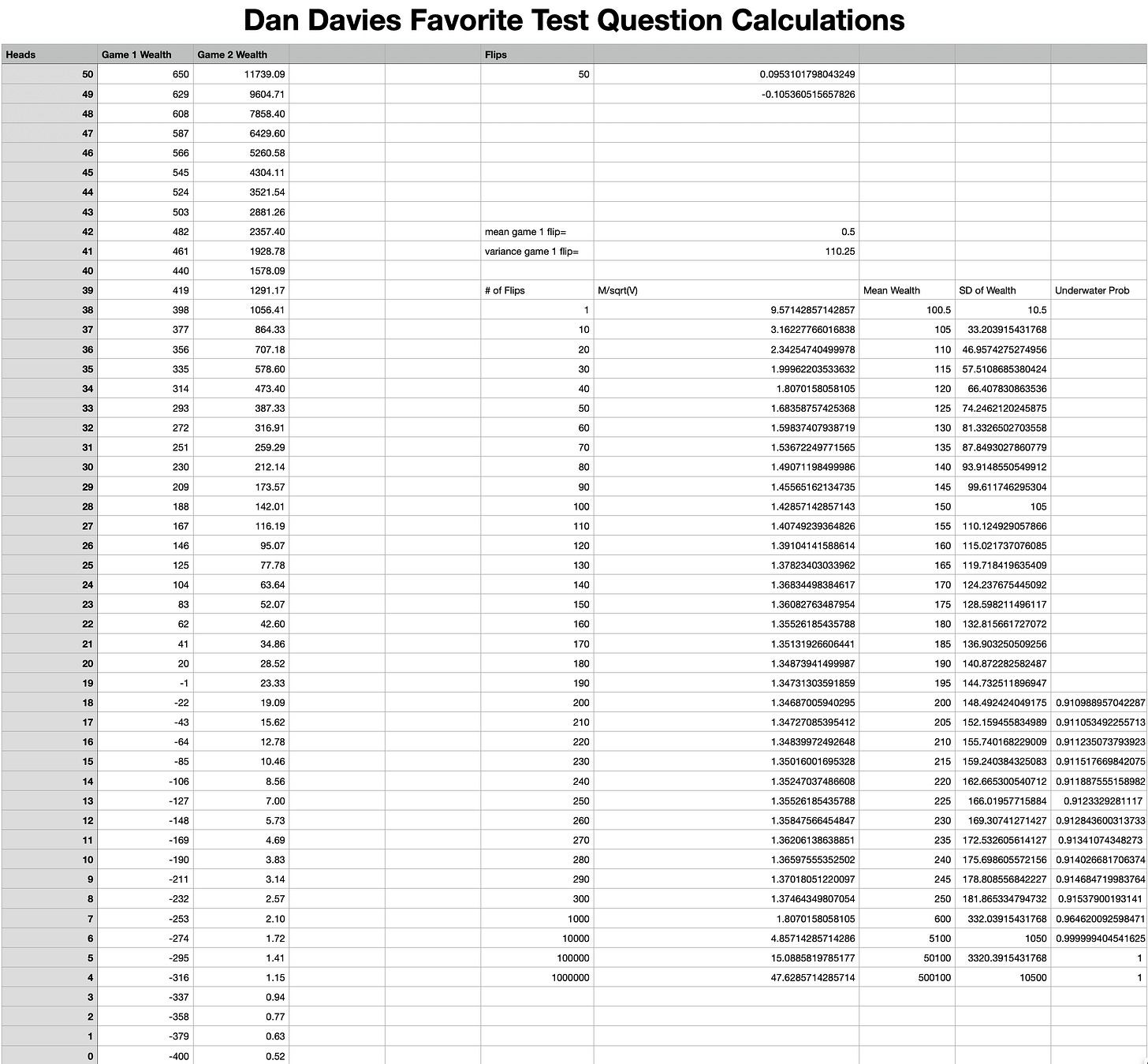
NOTE: I should note that I did extend Game 1 out further beyond 50 periods. Since there isn’t (really) an absorbing barrier at 0 because you could always gamble for resurrection over and over again with positive expected-value bets even if (though?) you do kiss the Bankruptcy Underwater Realm of King Neptune at some point, the question of whether you do hit zero at some point almost surely as the total number of periods T → ∞ is not all that interesting.

Dan Davies Fav Tq
16.4KB ∙ XLSX file
Download
Download

If I can still do math, I get that after 200 rounds of Game 1, your expected wealth is $200 and the standard deviation of wealth is sqrt(200)* 10.5 = 148.5, which means that your chances of being underwater (no absorbing barrier at wealth=0!) after 200 coin-flips are 9%. Thereafter that chance of being underwater at any snapshot moment decreases: after 10000 flips your chances of being underwater are 0.00006%.

If I can still do math, that is...

Share Brad DeLong's Grasping Reality

Leave a comment

Subscribe now

If reading this gets you Value Above Replacement, then become a free subscriber to this newsletter. And forward it! And if your VAR from this newsletter is in the three digits or more each year, please become a paid subscriber! I am trying to make you readers—and myself—smarter. Please tell me if I succeed, or how I fail…
#chatgpt5-vs-dan-davies-who-is-the-matador-and-who-is-the-bull-here
<https://braddelong.substack.com/p/chatgpt5-vs-dan-davies-who-is-the>